Mit der empirischen Verteilungsfunktion kann man die Frage beantworten, wie groß der Anteil an Daten ist, der kleiner oder gleich einem interessierenden Wert ist. Als Beispiel dient dazu die folgende Tabelle:
| Preis | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 |
| Häufigkeit | 5 | 5 | 10 | 15 | 18 | 9 | 8 | 6 | 4 |
| Häufigkeit + Häufigkeit < Preis | 5 | 10 | 20 | 35 | 53 | 62 | 70 | 76 | 80 |
| empirische Verteilung | 0,0625 | 0,125 | 0,25 | 0,438 | 0,663 | 0,775 | 0,875 | 0,95 | 1 |
Die Tabelle zeigt 9 verschiedene Preise eines Marktes, in diesem Fall des USD/CAD. Alle Werte in dieser Tabelle sind fiktiv und dienen ausschließlich zur Erklärung. Die Preise weisen eine Nachkommastelle auf und haben eine Range von 1.0 bis 1.8. Um die empirische Verteilung zu ermitteln, zählt man nun das Vorkommen der einzelnen Werte. In der oberen Tabelle kommt 1.0 genau 5 mal vor und ist der kleinste Wert. Das heißt, es gibt keine Werte, die noch darunter liegen. Also ist Häufigkeit + Häufigkeit < Preis ebenfalls 5 für 1.0.
Der Preis 1.1 kommt auch 5 mal vor, jedoch haben wir diesmal schon 5 Werte die darunter liegen (die der 1.0). Das heißt, Häufigkeit + Häufigkeit < Preis ist in diesem Fall 10.
1.2 kommt 10 mal vor. Da wir schon 10 Werte haben, die noch darunter liegen ist die Häufigkeit + Häufigkeit < Preis = 20. Das ganze führen wir bis zum Ende der Tabelle fort.
Wir ermitteln die Anzahl der einzelnen Preise und addieren im zweiten Schritt noch die Anzahl der Werte dazu, die darunter liegen. Wenn wir damit fertig sind, ermitteln wir die Verteilung, indem wir die kumulierten Werte (Häufigkeit + Häufigkeit < Preis) durch die gesamte Anzahl der Preise Teilen.
Was wir jetzt erhalten ist die Antwort auf die Frage wie groß z.B. der Anteil des Preises 1.5 ist. Dieser liegt bei 0,775. Umgerechnet sind das rund 78%. Das heißt 78% der Preise des USD/CAD lagen bei 1.5 oder darunter.
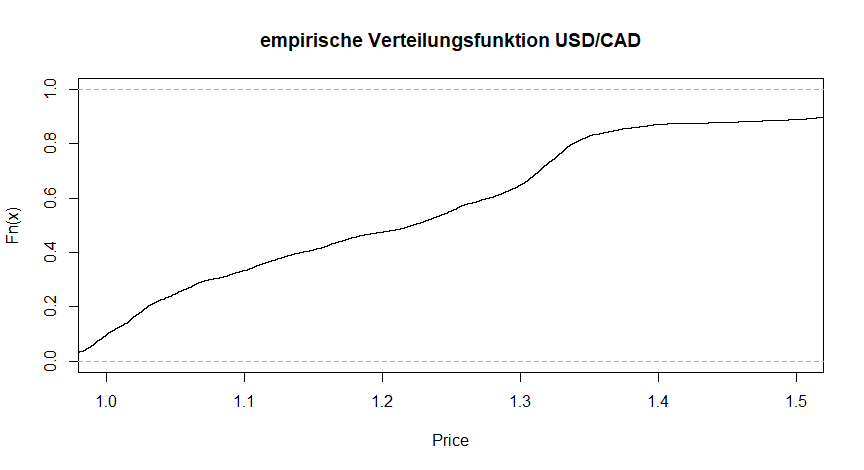
Grafisch stellt sich das ganze folgendermaßen dar:

Da wir in diesem Beispiel nur wenige Werte für die Auswertung verwendet haben, wirkt das ganze gestückelt. Verwenden wir die Preise des USD/CAD der letzten zehn Jahre erhalten wir eine glatte Verlaufskurve: